El tamaño de la muestra dependerá de las decisiones estadísticas y no estadísticas del investigador, pueden incluir por ejemplo la disponibilidad de los recursos, el presupuesto o el equipo que estará a cargo.
Antes de calcular el tamaño de la muestra se necesita determinar varias cosas:
- Tamaño de la población. Una población es una colección bien definida de objetos o individuos que tienen características similares. Cuanto mayor sea la población, menor será el tamaño de muestra necesario para obtener resultados precisos. Existen dos tipos:
- Población objetivo, que suele tiene diversas características y también es conocida como la población teórica. Dependiendo de la población que queramos estudiar, podremos necesitar un tamaño de muestra mayor o menor. Por ejemplo, si queremos hacer un estudio sobre los hábitos de consumo de un grupo muy específico de personas, podríamos necesitar un tamaño de muestra mayor para asegurarnos de que los resultados sean representativos.
- Población accesible es la población sobre la que los investigadores aplicaran sus conclusiones. Si es difícil acceder a la población objetivo, es posible que tengamos que aumentar el tamaño de la muestra para asegurarnos de tener suficientes datos.
- Margen de error (intervalo de confianza). El margen de error es una estadística que expresa la cantidad de error de muestreo aleatorio en los resultados de una encuesta, es decir, es la medida estadística del número de veces de cada 100 que se espera que los resultados se encuentren dentro de un rango específico. Cuanto menor sea el margen de error que queramos, mayor será el tamaño de la muestra necesario.
- Nivel de confianza. Son intervalos aleatorios que se usan para acotar un valor con una determinada probabilidad alta. Por ejemplo, un intervalo de confianza de 95% significa que los resultados de una acción probablemente cubrirán las expectativas el 95% de las veces. Cuanto mayor sea el nivel de confianza que queramos tener en los resultados, mayor será el tamaño de la muestra necesario.
- La desviación estándar. Es un índice numérico de la dispersión de un conjunto de datos (o población). Mientras mayor es la desviación estándar, mayor es la dispersión de la población. Cuanto mayor sea la desviación estándar de la población, mayor será el tamaño de la muestra necesario para obtener resultados precisos.
Es importante tener en cuenta que el tamaño de la muestra también está relacionado con el poder estadístico, que es la probabilidad de detectar una diferencia real entre dos grupos o un cambio en una variable a lo largo del tiempo. Cuanto mayor sea el tamaño de la muestra, mayor será el poder estadístico y por tanto mayor será la probabilidad de detectar diferencias o cambios reales.
Cálculo del Tamaño de la Muestra desconociendo el Tamaño de la Población
Si no conocemos el tamaño de la población, es posible calcular el tamaño de la muestra utilizando una fórmula que tiene en cuenta el tamaño de la población objetivo, el nivel de confianza deseado y el margen de error aceptable.
La fórmula para calcular el tamaño de muestra cuando se desconoce el tamaño de la población es la siguiente:
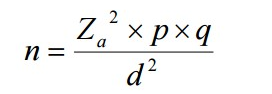
Donde:
n = Tamaño de la muestra
Z = Nivel de confianza, Valor de la distribución normal estandarizada para el nivel de confianza deseado. Por ejemplo, para un nivel de confianza del 95%, Z sería 1,96.
p = probabilidad de éxito, o proporción esperada, Proporción de la población que se espera que tenga la característica de interés. Si no se conoce, se puede asumir un valor de 0,5.
q = probabilidad de fracaso (1-p)
D = precisión (error máximo admisible en términos de proporción). Margen de error aceptable en términos de porcentaje. Por ejemplo, si queremos un margen de error del 5%, e sería 0,05.
Es importante tener en cuenta que esta fórmula solo se aplica cuando no se conoce el tamaño de la población y se supone que es grande en comparación con el tamaño de la muestra. Si conocemos el tamaño de la población, existen otras fórmulas más precisas para calcular el tamaño de la muestra.
Cálculo del Tamaño de la Muestra conociendo el Tamaño de la Población
El tamaño de la muestra es el número de elementos que se seleccionan de una población para participar en un estudio o investigación. El cálculo del tamaño de la muestra es importante porque una muestra demasiado pequeña puede no ser representativa de la población y, por lo tanto, dar lugar a resultados poco precisos. Por otro lado, una muestra demasiado grande puede ser costosa y tardar mucho tiempo en recopilar y analizar los datos.
La fórmula para calcular el tamaño de muestra cuando se conoce el tamaño de la población es la siguiente:
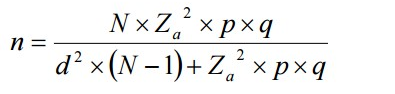
Donde:
N = tamaño de la población
Z = nivel de confianza
P = probabilidad de éxito, o proporción esperada
Q = probabilidad de fracaso
D = precisión (Error máximo admisible en términos de proporción).
Referencias
https://www.psyma.com/company/news/message/como-determinar-el-tamano-de-una-muestra
http://asignatura.us.es/dadpsico/apuntes/TamMuestra.pdf
¿Qué es y para qué sirve el Intervalo de Confianza? LadisLao P. díaz BaLL ve, Fernando G. ríos, MarceLa Mariano
